RakunBear
2025. 2. 25. 22:08
2025. 2. 25. 22:08
1.1 벡터
- 정의 : 크기(
magnitude)와 방향(direction)을 모두 가진 수량(quantity)
- 공식적으로
maginitude와 direction을 모두 가진 quantity를 벡터 값 수량(vector-valued quantity) 이라 부름.
- ex ) 힘(force), 변위(displacement), 속도(velocity)
- 표현 : 지향 선분(directed line segment)
- 길이 = 크기
- 화살표 = 방향
- 위치는 중요 X <- 위치의 변화는 벡터의 크기, 방향을 변화 시키지 않음
- 상등(equal) 조건 :
- 문자 표현 (원점 좌표 기준)
- v = (x, y, z)
- 원점에서 시작할 경우, 끝 좌표를 알면
direction과 magnitude를 알 수 있음
1.1.1 벡터 좌표계
- 기준계에 따라 벡터의 좌표는 다름
- 왼손잡이 좌표계 vs 오른손
-

1.1.2 기본 벡터 연산
- *$u = (u\{x}, u_{y}, u_{z})$ *$v = (v\{x}, v_{y}, v_{z})$
- $u_{x} = v_{x},; u_{y} = v_{y},; u_{z} = v_{z}$ 일 때에만 u = v
- 벡터 덧셈은 성분 끼리 이루어짐. (같은 차원의 벡터 끼리만 가능)
- 벡터에 스칼라(scalar, 크기만 있는 수량)을 곱하면, 결과는 벡터
- **$ku = (ku_{x}, ku_{y}, ku_{z})$
- 벡터 뺄셈은 벡터 덧셈과 스칼라 곱셈을 통해 정의
- $v − u = v + (−1 · u) = v + (−u) = (v_{x} − u_x, v_y − u_y, v_z − u_z)$
- 벡터의 뺄셈은
u 에서 v로 가는 벡터에 해당

1.2 길이와 단위 벡터
- 벡터의 크기 표현(Scalar) :
||u||
- $||u|| = \sqrt{y^2+x^2 + z^2}$
- 단위 벡터(unit vector)
- 크기가 1인 벡터
- 정규화(normalization)를 통해 만듦
- $\hat{v} = \frac{u}{||u||}$
1.3 내적 (inner product)
- 결과가 스칼라로 나옴
- $\mathbf{u} \cdot \mathbf{v} = u_x v_x + u_y v_y + u_z v_z$
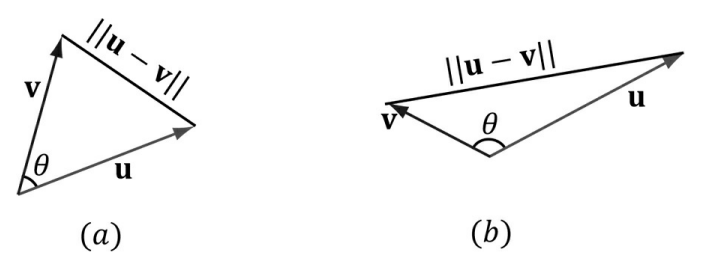
- $\mathbf{u} \cdot \mathbf{v} = ||\mathbf{u}||;||\mathbf{v}||\cos{\theta}$
- 벡터의 내적이 벡터 사이의 각도의 코사인을 벡터 크기로 비례한 것임을 뜻 함
- **(벡터(u) $\cdot$ 단위벡터($\hat{n}$))x$\hat{n}$ = u를 $\hat{n}$방향 투영 벡터
- 속성
- $\mathbf{u} \cdot \mathbf{v} = 0$ 이면 $\mathbf{u} \perp \mathbf{v}$ 직교
- $\mathbf{u} \cdot \mathbf{v} > 0$ 이면, 사이각은 90도 보다 작음
- $\mathbf{u} \cdot \mathbf{v} < 0$ 이면, 사이각은 90도 보다 큼
- 1.3.1 직교화
- 정규직교(orthonormal) : 모든 벡터가 단위 벡터이고, 서로 직교
- 직교화(orthogonalization) : 정규직교벡터 집합으로 만드는 것
- 그람-슈미트 직교화
- 기본 단계 : $w_0 = v_0$ 설정
- $1 ; <= ; i ; <= ; n-1$ 에 대해, $w_i = v_i - \sum_{j=0}^{i-1}proj_{w_j}(v_i)$
- 정규화 단계 : $w_i = \frac{w_i}{||w_i||}$

1.4 외적 (outer product)
- 두 벡터가 이루는 평면에 수직인 벡터를 생성하는 연산
- 결과는 벡터
- 외적의 계산은 일반적으로 오른손 좌표계를 기준으로 계산됨
- 왼손 좌표계의 경우, 부호를 바꿔줄 필요가 있음
- 왼손 엄지 법칙 : 엄지는 기준 벡터, 나머지 손가락은 남은 벡터, 손바닥은 생성되는 결과 벡터 방향
- $\mathbf{w} = \mathbf{u} \times \mathbf{v} = \begin{vmatrix} \mathbf{i} & \mathbf{j} & \mathbf{k} \\ u_x & u_y & u_z \\ v_x & v_y & v_z \\ \end{vmatrix} = \left( u_y v_z - u_z v_y, u_z v_x - u_x v_z, u_x v_y - u_y v_x \right)$
- 외적에는 교환법칙 성립x

번외
- 병진 이동(translation) : 상하좌우로 평행 하게 이동하는 것.
- 역벡터(inverse vector) : 벡터의 방향을 반대로 한 벡터
- 더하기의 항등원 : 벡터 + 역베터 = 영벡터
- $\mathbf{v} + (-\mathbf{v}) = \mathbf{0}$
- 벡터의 거듭제곱 : 벡터와 역벡터의 크기는 동일, 방향은 반대
- 영벡터(zero-vector) : 성분들이 모두 0인 벡터
- 정규화(normalization) : 임의의 벡터를 단위 벡터로 만드는 것
- 코사인 유사도(Cosine Similarity) : 내적공간의 두 벡터간 각도의 코사인값을 이용하여 측정된 벡터간의 유사한 정도
삼각함수 보각







